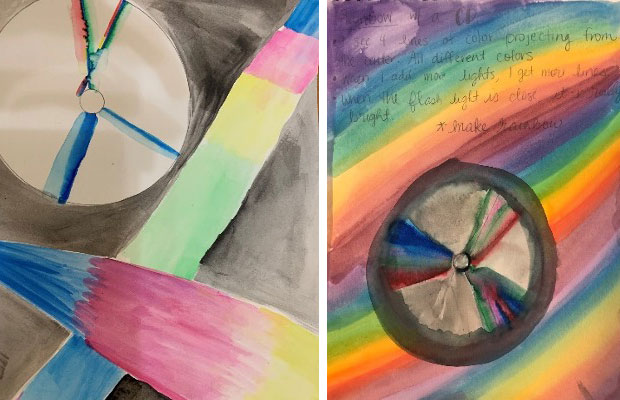Circuitry & Dance

Program Description

This program was originally a 6-day unit on circuitry and dance. Because of Covid-19, it was adjusted to fit a virtual audience. Students looked at the elements of dance through the concept of a simple circuit.

Learning Targets

“I Can…”

• Explain how a circuit works.
• Explain the elements of a circuit and how they work together.
• Relate the elements of a circuit to dance elements.
• Communicate a message through choreography and movement.

Essential Questions

• How are circuits & choreography related?
• How can I use movement to illustrate the concept of a simple circuit?

Curriculum Standards

S5P2. Obtain, evaluate, and communicate information to investigate electricity.
b. Design a complete, simple electric circuit, and explain all necessary components.
c. Plan and carry out investigations on common materials to determine if they are insulators or conductors of electricity.

S8P2. Obtain, evaluate, and communicate information about the law of conservation of energy to develop arguments that energy can transform from one form to another within a system.
b. Plan and carry out an investigation to explain the transformation between kinetic and potential energy within a system (e.g., roller coasters, pendulums, rubber bands, etc.).
d. Plan and carry out investigations on the effects of heat transfer on molecular motion as it relates to the collision of atoms (conduction), through space (radiation), or in currents in a liquid or a gas (convection).

Arts Standards

ESD4.CR.1 Demonstrate an understanding of the choreographic process. 

1. Explore a variety of choreographic structures, forms, and designs (e.g. AB, ABA, canon, call-response, narrative, complementary/contrasting shapes, symmetry).
2. Demonstrate proper dance technique while performing choreography.

Implement the use of props within choreography.

ESD4.CR.2 Demonstrate an understanding of dance as a form of communication.

a. Use movement to express an idea or feeling.

b. Understand how theatrical elements (e.g. costuming, lighting) contribute to the meaning of dance.

Content Vocabulary

• Source: A supply of moving electrons
• Voltage: electromotive force or potential difference expressed in volts.
• Resistance: A physical property of materials. If a material has a high resistance, it opposes the passage of a steady electric current. The lower the resistance, the easier it is to force electrons to leave atoms and move through the material.
• Load: A component that consumes power supplied by a power source.
• Current:  the time rate of flow of electric charge
• Wire: filament made of flexible metal
• Conductor: creates a pathway for electrons
• Insulator:  prevents the flow of electrons
• Pathway: a path, course, route, or way for an electrical current to flow

Arts Vocabulary

• Level: one of the aspects of movement (high, middle, low)
• Pathway: designs traced on the floor or through the air as a dancer moves through space.
• Sustained Movement: smooth and unaccented.
• Suspended Movement: occurs in a moment of resistance to gravity.
• Percussive Movement: movement with sharp starts and stops.
• Vibratory Movement: movement with rapid, repeated bursts of energy.
• Swimming Movement: movement with a repeated cycle of fall and recovery like a pendulum.
• Locomotor: movement that travels through space.
• Non-Locomotor: movement that does not travel through space.

Summative Assessment

• Students create a paper circuit that works using series circuit concepts.
• Students create a wearable circuit using the LilyPad Arduinos and conductive thread.
• Students create choreography that demonstrates the concept of energy traveling through a circuit

Materials

• LEDs
• Copper Tape
• Paper (card stock*, copy paper, construction paper)
• Coin Cell Batteries (one per person)
• Conductive Thread
• Lilypad LEDs
• Felt
• Thread
• Sewing Needles
• Battery holders
• Makey Makeys

*preferred

Visual Arts Activating Strategy (5-10 min)

Each day we began our class with a 15-minute dance-inspired warm-up exercise. The purpose of this activating strategy is to get their heart rates up and have them working with some of the dance skills we will be using throughout the program.

Visual Arts Main Activity

PROCESS:

Day 1:

• Warm up
• Group discussions “What is a circuit”
  • This discussion focused on a simple circuit (switch, wire, power source, load)
• Group tested out ideas of what each element would look like as a movement.
• Group discussed Alternating Currents vs Direct Current.
• Group created a circuit movement inspired by an Alternating Current Circuit.  Each element in the circuit was expressed through movement and put together to form simple choreography.
• STEM Connection
  • Students created “Paper Circuits” using copper tape, an LED, and a coin cell battery. This demonstrated the simple circuit we learned about.

Day 2:

• Warm up
• Group review of “What is a circuit”
• Students performed group choreography illustrating AC created the previous day.
• Group discussed Source, Voltage, Resistance, and Load.
• Each student created a movement to represent each of these vocabulary words.
• Students taught each other their movements.
• Students were assigned to practice overnight.
• STEM Connection
  • Students used various objects to explore with Makey Makeys.

Day 3:

• Warm up
• Group review of “What is a circuit” and shared what they created the day before.
• Teacher put the choreography together and students created and practiced a dance to illustrate the power of circuitry.
• Students used an Electric Circuit toy to create a human circuit as part of their choreography.
• Students listened to various songs to choose the music that best related to their choreography.
• STEM Connection
  • Students learned about wearable circuits and began working on their own design.

Day 4 (Online):

• Warm up/ Introduce specific dance movement (~30 minutes) (Clip)
• Group review of circuitry vocabulary.
• Students were given 5 minutes to create a new movement for their circuit vocabulary.
• Students shared out.
• Group review of what was in their bags (Felt, Coin Cell Batteries (one per person), Conductive Thread, Lilypad LEDs, Felt, Thread, Sewing Needles, & Battery holders for the long-term project to create a wearable circuit)

Day 5:

• Warm up/ Introduce specific dance movement (~30 minutes)
• Group review of circuitry vocabulary.
• Group review of paper circuits and Series vs Parallel circuits.
• Students created “Positivity Posters” using the Paper Circuits
• Students also created movements that represent the message conveyed in the Positivity Poster.
• Demonstration of how to create a paper circuit. (Clip)

Day 6:

• Warm up: Students are led through a warmup
• Vocabulary review in choreography- Source, current Load current source
• Student shared Positivity Poster and Choreography (Clip)
• Group Performed student choreography (Clip)

Reflection Questions

• What do we know about circuits?
• How did our paper circuits reflect our choreography?
• How did your positivity poster and choreography work together?

Additional Resources

• Presentation: https://docs.google.com/presentation/d/13Umx74O7H56xMZDpeZ9xW9o6lcjYM51FRulnt3fRiS8/edit?usp=sharing
• Wearable/Soft Circuit Info: https://drive.google.com/file/d/1r4PjKADfZPrarTGzLzNXtpXk2YoByuCi/view?usp=sharing

Light & Sound

Description

In this program, we investigated Light and Sound through STEM activities, visual art, music, and dance.

Learning Targets

“I Can…”

• Explain reflection and refraction.
• Explain how pixels work together to give off colors.
• Describe how sound waves move and how frequency is related to the sound an object produces..
• Show how lighting and sound affects a piece of choreography.
• Demonstrated how transparent, translucent, and opaque work together in visual art.

Essential Questions

• How can I obtain, evaluate, and communicate information about the nature of light and how light interacts with objects?
• How can I obtain, evaluate, and communicate information about how sound is produced and changed and how sound and/ or light can be used to communicate?
• How can I develop and use a model to compare and contrast how light and sound waves are reflected, refracted, or absorbed through various materials?
• How can I develop and use a model to illustrate how transparent, translucent, and opaque materials work in relation to light?

Curriculum Standards

S4P1. Obtain, evaluate, and communicate information about the nature of light and how light interacts with objects.

1. Plan and carry out investigations to observe and record how light interacts with various materials to classify them as opaque, transparent, or translucent.
2. Plan and carry out investigations to describe the path light travels from a light source to a mirror and how it is reflected by the mirror using different angles.
3. Plan and carry out an investigation utilizing everyday materials to explore examples of when light is refracted. (Clarification statement: Everyday materials could include prisms, eyeglasses, and a glass of water.

S4P2. Obtain, evaluate, and communicate information about how sound is produced and changed and how sound and/or light can be used to communicate.

1. Plan and carry out an investigation utilizing everyday objects to produce sound and predict the effects of changing the strength or speed of vibrations.
2. Design and construct a device to communicate across a distance using light and/or sound.

S8P4. Obtain, evaluate, and communicate information to support the claim that electromagnetic (light) waves behave differently than mechanical (sound) waves.

1. Develop and use a model to compare and contrast how light and sound waves are reflected, refracted, absorbed, diffracted or transmitted through various materials. (Clarification statement: Include echo and how color is seen but do not cover interference and scattering.)

Arts Standards

VA4.CR.1 Engage in the creative process to generate and visualize ideas by using subject matter and symbols to communicate meaning.

VA4.CR.2 Create works of art based on selected themes.

VA4.CN.3 Develop life skills through the study and production of art (e.g. collaboration, creativity, critical thinking, communication).

VA5.PR.1 Plan and participate in appropriate exhibition(s) of works of art to develop the identity of self as artist.

VA5.CN.3 Develop life skills through the study and production of art (e.g. collaboration, creativity, critical thinking, communication).

VA6.CR.1 Visualize and generate ideas for creating works of art.

VA6.CR.3 Engage in an array of processes, media, techniques, and/or technology through experimentation, practice, and persistence.

VA6.CR.6 Keep an ongoing visual and verbal record to explore and develop works of art.

VA6.PR.1 Plan, prepare, and present completed works of art.

VA7.CR.1 Visualize and generate ideas for creating works of art.

VA7.CR.2 Choose from a range of materials and/or methods of traditional and contemporary artistic practices to plan and create works of art.

VA7.CR.3 Engage in an array of processes, media, techniques, and/or technology through experimentation, practice, and persistence.

VA7.PR.1 Plan, prepare, and present completed works of art

VA8.CR.1 Visualize and generate ideas for creating works of art.

VA8.CR.2 Choose from a range of materials and/or methods of traditional and contemporary artistic practices to plan and create works of art.

VA8.CR.3 Engage in an array of processes, media, techniques, and/or technology through experimentation, practice, and persistence.

ESD4.CR.1 Demonstrate an understanding of the choreographic process.

ESD4.CR.2 Demonstrate an understanding of dance as a form of communication.

ESD4.PR.4 Understand and apply music concepts to dance.

ESD4.CN.3 Integrate dance into other areas of knowledge.

ESD5.CR.1 Demonstrate an understanding of the choreographic process.

ESD5.PR.2 Understand and model dance etiquette as a classroom participant, performer, and observer.

ESD5.PR.4 Understand and apply music concepts to dance. a. Demonstrate and create movement in response to a variety of musical selections. b. Demonstrate musicality while performing dance phrases.

ESD5.RE.1 Demonstrate critical and creative thinking in dance.

MSD.PR.4 Understand and apply music concepts to dance.

MSD.RE.1 Demonstrate critical and creative thinking in dance.

MSD.CR.2 Demonstrate an understanding of dance as a form of communication.

MSD.CN.3 Demonstrate an understanding of dance as it relates to other areas of knowledge.

ESGM4.CR.1a. Improvise rhythmic question and answer phrases using a variety of sound sources.

ESGM4.PR.2a. Perform rhythmic patterns with body percussion and a variety of instruments using appropriate technique.

EESGM4.RE.1c. Identify and classify (e.g. families, ensembles) classroom, orchestral, American folk, and world instruments by sight and sound.

ESGM4.CN.1b. Discuss connections between music and disciplines outside the fine arts.

ESGM5.CR.1 Improvise rhythmic phrases.

ESGM5.PR.2a. Perform rhythmic patterns with body percussion and a variety of instruments using appropriate technique.

ESGM5.RE.1b. Describe music using appropriate vocabulary (e.g. fortissimo/pianissimo, presto/largo/moderato/allegro/adagio, legato/staccato, major/minor), intervals (e.g. step, skip, repeat, leap), timbre adjectives (e.g. dark/bright), and texture (e.g. unison/harmony).

ESGM5.RE.1c. Identify and classify (e.g. families, ensembles) classroom, orchestral, American folk and world instruments by sight and sound.

ESGM5.CN.1b. Discuss connections between music and disciplines outside the fine arts

MSGM6.RE.1a. Recognize and describe musical events in an aural example using appropriate musical terminology

MSGM7.CR.1b. Improvise simple rhythmic and melodic variations

MSGM7.RE.1a. Recognize and describe musical events in an aural example using appropriate musical terminology

MSGM8.CR.1b. Improvise melodic embellishments and simple rhythmic and melodic variations.

MSGM8.RE.1a. Recognize and describe musical events in an aural example using appropriate musical terminology

Content Vocabulary

• Reflection: the throwing back by a body or surface of light, heat, or sound without absorbing it.
• Refraction: A change of direction that light undergoes by passing obliquely through one medium.
• Sound: vibrations that travel through the air or another medium and can be heard when they reach a person's or animal's ear.
• Sound waves: a vibration of waves by which sound is projected.
• Pitch: the quality of a sound governed by the rate of vibrations producing it.
• Frequency: the number of occurrences of a repeating event per unit of time
• Pixel: an area of illumination on a display screen, many pixels compose an image.
• Digit: any of the numerals from 0 to 9.
• Digital: a series of the digits 0 and 1 represented by values of a physical quantity such as voltage.
• Additive color theory: starts without light (black) and light sources of various wavelengths combine to make a color.
• Subtractive color theory: starts with light (white), colored inks, paints, or filters between the light source subtract wave lengths from the light, give it color.
• Binary code: a coding system using the binary digits 0 and 1 to represent a letter, digit, or other character in a computer or other electronic device.
• Bits: a unit of information expressed as either a 0 or 1 in binary notation.
• RGB code: the RGB color model is an additive color model in which red, green, and blue light are added together in various ways to reproduce a broad array of colors.
• Electric circuit: a path in which electrons from a voltage or current source flow.
• Conductor: a material that transmits heat, electricity, or sound.
• Insulator: a substance which does not allow the full passage of heat or sound.
• Open circuit: an electrical circuit that is not complete.
• Closed circuit: an electrical circuit that is complete.

Arts Vocabulary

• Opaque: not able to be seen through; not transparent.
• Transparent: allowing light to pass through so that objects behind can be distinctly seen.
• Translucent: allowing light, but not detailed shapes, to pass through; semitransparent.
• Literal movement: Movements that show exact meaning and actions.
• Abstract movement: symbolic movement.
• Choreography: the sequence of steps and movements in dance
• Levels of Dance (low, middle, high): The three levels in dance movement are high, middle and low.
• Percussive: This refers to a quality of movement characterized by sharp starts and stops; staccato jabs of energy.
• Rhythm: a strong, regular, repeated pattern of movement or sound.
• Mood: atmosphere that evokes certain feelings or vibes
• Pitch: highness or lowness of sound.
• Timbre: distinctive quality of sounds; the tone color or special sound that makes one instrument or voice sound different from another.

Materials

Materials Provided by Teachers

• Two Plastic Bottles (approximately 12-16 oz in size)
• Masking Tape (one roll)
• Foil (1-2 foil sheets or approximately one foot from a roll)
• Teaspoon of Uncooked Rice
• Five rubber bands
• Ziplock baggies to package materials for students
• Lamination Pocket, laminated (cut one piece in half, students need ½ apiece)
• Grid paper
• One Small Bottle of Food Coloring
• Alka Seltzer (one tablet per student)
• Four LED lights
• Two Coin Battery per student
• One Bottle of Liquid Glue per student
• One Piece of Cardstock
• Journal
• Pencil
• Markers
• CD
• Flashlight
• Watercolor paint
• Watercolor paper
• Clear tape
• Kaleidoscope Kit
• Colored paper (three half-sheets of assorted colors)
• Plastic sheets (three half-sheets of assorted colors, you may cut plastic notebook dividers for these)
• One Roll of Plastic tape

Materials Students Provided at Home

• Large Box
• Scissors
• Bowl
• Saran Wrap
• Objects from around the house (tissue boxes, toilet paper tubes, etc.)
• Salt
• Newspaper (to protect surfaces)
• Vegetable oil
• Shaker Object (pack of tic tacs or bottle of sprinkles, etc.)
• Grocery Bag

Activating Strategy (5-10 min)

Day 1 AM Session:

• Introduce Light Refraction with Jar & Pencil Activity
  • Fill a clear container with water.
  • Tell the students you will be placing the pencil in the water.
  • Ask the first question.
  • Place the pencil in the water.
  • Give students a few moments to make observations.
• Ask the following questions:
  • What do you think is going to happen?
  • What do you observe?
  • What do you believe is causing the “bent/ split” pencil illusion?
  • Introduce the word refraction

Day 1 PM Session:

• Review the Light Box Magic STEM challenge from the morning session and allow students to discuss their observations/ discoveries
  • How the amount of light in the box may change with different amounts of water, different time of day, blocking the top side of the bottle, etc?
  • Light Box Example
• Investigate the CD with reflections of light using house lighting and the flashlight provided
  • Possible questions to ask: What shapes and colors do you see in the rainbow?  What do you notice when you use two CDs? What do you notice when you put the flashlight close to the CD?
  • How does the CD act as a prism?
  • Allow students to write their observations in their journals.
  • Investigating Light

Day 2 AM Session:

• Ask students the following questions to prompt discussions verbally or in the chat
  • What do you think of when you hear the word sound?
  • What do you think of when you hear the word waves?
• Discuss that sound is made of vibrations and invisible soundwaves
• Demonstrate and have students complete dancing sprinkles/ rice activity at the same time to demonstrate how you can “see” soundwaves
• Sound Waves Example
• Discuss how sound waves travel, how vibrations are recognized as different sounds, and how the size and shape of the sound waves determine the kind of sound heard.
• Review various musical instruments, homemade and traditional. Have students compare and predict sounds of these instruments and how the sounds (vibrations) were created.
• Have students find a way to create sound using objects around them and improvise an 8-beat pattern using that object.
• Have students create an 8-beat pattern and repeat it. Add to YouTube backing track.

Day 2 PM Session:

• Students will share their instruments they created after the morning STEM challenge.  Play eight beats of music together as a group/ class.
• Discuss as a class the following questions
  • What is a shadow?
  • How might artists use shadows?
  • Possible answers: to make things look more realistic, to add depth, etc
• Find a shadow in your house and spend five minutes sketching the object and its shadow in your journal with a pencil.

Day 3 AM Session:

• Review shadow sculptures from the end of Day 2
• Introduce how sound is related to dance
• Students will watch a clip from Broadway’s STOMP to get students thinking about how sound is used in dance.  Video: STOMP - Established in 1994 NYC
  • Ask students what common household instruments they see in the video.

Day 3 PM Session:

• View images of Yayoi Kusama’s work.  Students will discuss in chat what they observe/ notice about her work. (mirrors, reflections, infinity rooms, duplicates, etc)
• What makes her work unique?
• What themes do you notice?

Day 4 AM Session:

• Introduction to vocabulary words transparent, translucent, and opaque by making a lava lamp. Possible questions to ask:
  • After pouring the water and oil into the glass, what do you believe is going to happen when food coloring is added? Will it mix with the water, oil, or both?
  • What do you observe when you initially add the food coloring?
  • If you continue to add food coloring to the water, will the water stay transparent or translucent?
• Example

Day 4 PM Session:

• Briefly discuss what an electric circuit is and what materials are used/needed to make a complete (closed) circuit
• Show students how to use a coin battery to illuminate a LED light
• STEM Challenge: LED Glue/ Salt Circuit
  • Gather materials: half piece of cardstock, coin battery, LED light, glue, salt and tray/ paper plate to work over
  • Fold the corner of your paper up to make a “switch”
  • “Draw” a line using glue from the folded corner of the paper and then towards the edge.  Be generous with the glue
  • Skip a space for your LED and continue your glue line back near the folded corner
  • add your LED to the space making sure the “legs” are in the glue
  • sprinkle a good layer of salt on the glue.  Lift the paper and dump the extra salt on the tray
  • When it is dry, use the coin cell battery to try and light up your LED
  • **The salt circuit is not a very strong circuit. The light will be dim. You may try paper circuits with copper tape for a brighter light.

Example

Main Activity

Day 1 AM Session: 

• Students were introduced to the concept of light refraction during the activating strategy.
• Students watched a video “Liter of Light” to be inspired by how light refraction is being used in 3rd World countries to reduce electricity costs for families.
• Students STEM activity was to create a way to light up a “room” using light refractions.
• Teachers demonstrated how to create a Light Box to demonstrate this concept.

• Step 1: Gather your materials
• Step 2: Fill your bottles with water (Add a few drops of food coloring if you want!)
• Step 3: Trace the bottom of the bottles on the top of the box and carefully (and with a parent/older siblings help) cut holes.  Put tinfoil on the top of the box, covering the holes. Poke a hole in the foil over the open. This will help the light reflect into the bottles.
• Step 4: Carefully (and with a parent/older siblings help) cut a hole in the side of the box to look inside.  We recommend cutting a smaller window or just eye holes.
• Step 5: Push bottles into holes and look in the viewing window.
• Example

Adapted from: https://www.trueaimeducation.com/light-box-magic/

• Teachers demonstrated the relationship between colors and math (seeing the numbers in digital media). The following topics were discussed:
  • What does the word digital mean?
  • Pixels-comparing LED & LCD close up images of digital screens
  • Additive Color Theory vs Subtractive Color Theory
  • Teacher demonstrates a “large scale pixel” by using three lights (red, green, and blue bulbs)
  • Discuss how every pixel has three parts (red component, green component, and blue component)
  • Discuss how each pixel receives three digital (mathematical) signals--one signal for how much red light, how much green light, and how much blue light
  • Discussion of how number values in ColorMath are based on binary code
  • 8-bit Color: An RGB Code has 3 values (256 possible red values, 256 green values, and 256 blue values)
  • Presentation
• Students can create their own digital art using https://paintz.app

Day 1 PM Session:

• Students experimented with a flashlight and CD in the activating strategy.
• After completing the investigation, instruct students trace the CD on a piece of watercolor paper
• Students will use markers to draw the “lines/ rainbows” created by the flashlight against the CD.  Students may use their paint brush to paint water on top of the marker to use as a watercolor option (water of the washable markers acts like watercolor.
• Students may then use the watercolor paint to paint outside of the CD showing what shapes and angles they see when observing the reflection of light against the CD
• Allow approximately 10-15 minutes for students to paint their observations followed by a share out

Examples:

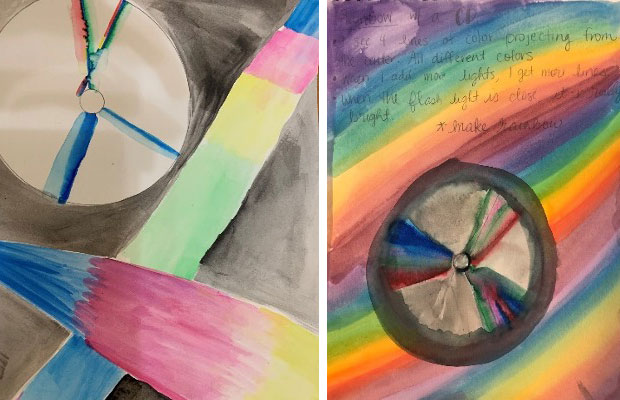
Day 2 AM Session: 

• After introducing sound and soundwaves in the activating strategy, introduce the vocabulary word pitch.  You may do this by playing different sounds on an instrument
• Show students a variety of instruments (these may be real instruments or instruments created from household/ classroom objects
• Example
• Allow students to find an object to create an instrument out of to play a beat (for example: pencil and water bottle make a drum, using spices/ sprinkles as a shaker)
  • using the instrument they create, play 8 beats together (all playing one note at the same time) followed by 8 beats of 8 counts of a beat of their choice
  • you may do this a few times to allow students to experiment with their instrument
• STEM Challenge: Create & build your own musical instrument using household items (rubber bands, rice, toilet paper/ paper towel rolls, etc.)
  • students will share out their instruments and play music together at the beginning of their afternoon session

Day 2 PM Session: 

• After sharing instruments and introducing shadows in the activating strategy, allow students to look at images of shadows made by sculptures
• Show clip video of (time 1:40-4:00): Tim Noble & Sue Webster, NO - Exhibition & Limited Editions
• Students are challenged with the task of creating a sculpture with household items that will create an interesting shadow.

Day 3 AM Session: 

• After reviewing shadow sculptures and dance clip in the activating strategy, discuss the following:
  • STOMP is performed in theaters, but it is not a play, musical, or opera. It is not theater in the traditional sense of the word. There is no speech, dialogue or plot. However, it does have two characteristics of traditional theater: mime and characterization. Each performer has an individual character which is distinct from the others. These characters are brought out through the mime and dance in the show.
  • The entire show is highly choreographed, interweaving dance into all its aspects. In STOMP, there is a symbiotic relationship between dance and music. The music is created within the dance, but the dance itself is dependent on the music for its rhythm and character. STOMP shows a true marriage of movement and music, where both create and enhance each other.
• Show second video: How To STOMP: Hands & Feet
  • Play the video a second time and ask students to mimic the dance moves taught in the video.  You may need to replay the video to allow
• Show third video: How to STOMP: Bags
  • Ask students to create their own rhythm using bags from their house and share out
• Show fourth video: How to STOMP: Breath Mints
  • Ask students to repeat the rhythm taught using something they can shake from their house (breath mints, spices, sprinkles, etc.)
• Show fifth video: STOMP Pancakes 1 #StompAtHome
• Think about all the different ways you made sound and the different ways you saw sound made in the STOMP videos.
  • Why do you think the different props made different sounds?
  • Challenge: Create your own STOMP inspired choreography using found sound.
• Clip
• STEM Challenge: Create Your Own Hologram
  • Follow directions of how to make a trapezoid pattern (see picture)
  • Cut out the pattern and trace four trapezoids on your clear plastic sheet
  • Cut out the four trapezoids and tape together four of the perpendicular lines to create a square pyramid.
  • Place your finished hologram on top of the video playing on your device
  • Example 1, Example 2

Day 3 PM Session:

• After introducing Kusama’s work and discussing reflections, have students build their kaleidoscope using the kaleidoscope kit.
• Allow students time to investigate and place different objects in the kaleidoscope to see how it appears.

Ask students to sketch what they see in their kaleidoscope in their journals

Day 4 AM Session:

• Discuss a Lighting Director’s role in dance and show Mark Stanley: Lighting the New York City Ballet
  • Discuss how light gives character to dance and creates the mood
  • Light can also do the following: create space, intensity, shapes, shadows, dimensions, etc.
• Discuss “What is mood? What are examples?”
  • Possible answers: mood is a literary element that evokes certain feelings or vibes in readers, but can be used the same way in dance
  • Examples of moods:  cheerful, reflective, gloomy, humorous, melancholy, whimsical, romantic, mysterious, ominous, calm, lighthearted, hopeful, angry, fearful, tense
• Discuss “How can you create mood with lights?”
  • colors (how they mix), shadows (what will happen when things are in front of the lights), angle, intensity, movement of light, layers of light, etc.
• Watch the following video clips and discuss what you believe the mood is and how did the lighting help create the mood?
  • Houston Ballet-Reveal-Garrett Smith Choreography
  • “Ounce of Faith” | Trailer | Alvin Ailey American Dance Theater
  • Trailer - IN Cognito Full Piece Premiere
• Dance Challenge: Think about how lighting affected the mood in the various performances and complete the following steps:
  • 1. Pick a mood (for example: cheerful)
  • 2. Create a movement phrase that matches your mood.
  • 3. Are there any adjustments you can make to the lighting in your space to match the mood of your choreography?  Example: brighter lights, dimmer, lights, use shadows, colored light, light coming in at a different angle, light movement.

Day 4 PM Session:

• After introducing circuits and completing LED salt/ glue circuit, show video clip of Tom Fruin’s work and allow students to type their observations in the chat
  • Video: Tom Fruin’s Large-Scale Sculptures, Icons of Brooklyn’s Public Spaces
  • Possible Observations: stained glass, shapes, quadrilaterals, shadows, colors, glass house, life-size, etc.)
• Ask students, “What do you need to make a shadow?”
  • Possible answers: light source, an object to block the sun, an opaque object, etc.
  • Why are some of the shadows in Tom Fruin’s work different colors?
  • Discuss transparent, translucent and opaque materials and how each respond to light.
• Sculpture Challenge: Make a 3D sculpture incorporating transparent, translucent and opaque materials inspired by Tom Fruin’s work.

Here are some snippets of student work throughout the week: VIDEO

Reflection Questions

• What colors did you feel worked together and why?
• What challenges did you have during this process?
• What tools worked best for your process and why?

TECHNOLOGY INTEGRATION (Include technology that is integrated directly into the project. Ex: apps, websites for research, virtual field trips, mystery skype calls, etc..)

Visual Arts Component - Pour Painting

Science and Visual Arts

Description

In this program, we will explore color, shape, fluidity, and light. Students will have a deeper understanding of how these elements work together to help an artist create their masterpieces. Through this process, students will be able to experiment with flow and shapes to create their artwork.

Learning Targets

“I Can…”

• create shade and tints with paint
• describe differences between mixing light and mixing paint colors.
• create works of art using a variety of household tools.

Essential Questions

• How do we manipulate our mediums to create abstract art?
• What effect does shape have on the movement of our medium?

Content Vocabulary

• Gravity: the force that attracts a body toward the center of the earth, or toward any other physical body having mass.
• 3-dimensional shape: a three-dimensional shape can be defined as a solid figure or an object or shape that has three dimensions – length, width and height.
• Edges: the outside limit of an object, area, or surface; a place or part farthest away from the center of something.
• Vertices: The common endpoint of two or more rays or line segments.
• Faces: In any geometric solid that is composed of flat surfaces, each flat surface is called a face. 
• Elevation: The angle of elevation of an object as seen by an observer is the angle between the horizontal and the line from the object to the observer's eye (the line of sight).
• Volume: can be defined as the 3-dimensional space enclosed by a boundary or occupied by an object. 
• Surface Area: The surface area of a solid object is a measure of the total area that the surface of the object occupies.
• Flow: formalizes the idea of the motion of particles in a fluid. 

• Viscosity: Viscosity is a physical property of fluids. It shows resistance to flow.

Arts Vocabulary

• Value: value refers to the visible lightness or darkness of a color.
• Shade: a shade is a mixture with black, which increases darkness. 
• Tint: a tint is a mixture of a color with white, which reduces darkness, 
• Primary: are basic colors that can be mixed to produce other colors. They are usually considered to be red, yellow, and blue.
• Secondary: a color resulting from the mixing of two primary colors.
• Tertiary: a color produced by an equal mixture of a primary color with a secondary color adjacent to it on the color wheel.

Summative Assessment

• Gallery presentation

• 100 Color Challenge
• 3-D sculpture 
• 3-5 Canvas experimentation paintings 
• Community paint pour
• property of fluids. It shows resistance to flow.

Materials

For Activating Activities

• Red Light
• Green Light
• Blue Light
• Paper
• Paper plate
• Paint (Acrylic)
  • Red
  • Yellow
  • Blue
  • Black
  • White
• Paint brushes
• Water
• Paper towels
• Pencil

For Main Activities

• Acrylic Paint
• Floetrol
• Various household tools for experimentation (chain, strainer, dust pan, cups, etc)
• Heat gun
• Silicon
• Canvas - variety of sizes
• blocks 

Activating Strategy (5-10 min)

Mixing Visual Light

Students went into the Black Box theater and created shadows using colored light. (Red, Green, and Blue) Students were able to see their shadows and what happens when you mix colored light. The result is a colored shadow.

Light is additive colors

Primary light colors are Red, Blue, and Green

• red light + green light makes yellow light
• red light + blue light makes purple light
• green light + blue light makes aqua (cyan) light
• blue light + red light makes pink (magenta) light
• red + blue + green makes white light

Clip

Students theorized what would happen when you mix pigment colors.

Main Activity

PROCESS:

Day 1:

Mixing Pigments

• Students participated in the 100 color challenge. Students were given a paper plate with red, yellow, blue, white, and black. Students drew 100 squares on a piece of paper and tried to create 100 different colors from the 3 primary colors plus black and white. 
• You can discuss shades (adding black) and tints (adding white).

When students are done with their plates of paint (palette) they can use scrap paper or cardboard to make a fun print! (See Image below)

• Clip 1
• Clip 2

Day 2:

• Finish 100 Color Challenge if needed.
• Students watched several videos for inspiration for the Acrylic Pour Painting. VIDEO
• Students explored the MakerSpace to find items to help build their 3-D sculpture.
• Students used foam board, cardboard, small wooden blocks, small foam blocks, and craft glue to design and build small sculptures.
  • Cutting out bases Clip
  • Designing sculpture Clip1, Clip2, Clip3
• Let the sculptures dry overnight.

As students finish their sculpture, they can work on their 100 color project or help prepare the acrylic paint & floetrol.

Day 3:

• Students prepared their sculpture for the addition of acrylic paint. Students chose colors and added floetrol and water to the acrylic base. This creates a fluid mix that flows easily.
• Students poured the paint over the sculptures.
• Students observed the flow of the paint for future paintings.
  • Students used shallow pans to hold their sculptures and collect any excess paint.
• Clip 1 - Process
• Clip 2 - Product

Day 4 & 5:

• Students chose a variety of canvases and tools and experimented with their paint pours.
  • Clip 1 - Cup pour
  • Clip 2 - experimenting with a heat gun
  • Clip 3 - Strainer pour
  • Clip 4 - Coke Bottle pour

Day 6:

• Students prepared their work as a Visual Arts Gallery.
• Students set up a table for visitors to try the 100 color challenge and set up for a community paint pour. This artwork was permanently installed in the school.

Video Recap of the program (played during the Gallery Opening): Video

Reflection:

• What colors did you feel worked together and why?
• What challenges did you have during this process?
• What tools worked best for your process and why?

Instructional Videos

• Reflection through Effective Questioning

Classroom Tips:

• If carpeted room, put down drop cloths or newspaper for painting.
• Room with no windows works great!

Reflection Questions

• What brush worked the best? Why?
• What did you change or improve on your brush while you were painting?
• What object helped you create the effect you needed for your type of galaxy?

Additional Resources

• Videos of paint pours: Link

Grade 7: African Studies

Unit Description

In this arts integrated unit, students will experience and understand the meaning of an African Welcome Dance specific to a tribe or region in Africa. They will compare and contrast traditional “Welcome” dances to modern “Step” dances. Students will incorporate modern dance into their personalized and original versions of a Tribal Welcome Dance. Within the visual arts component, students will create an African Mask. They will compare and contrast traditional masks and their role within African Masquerades to the work of contemporary artist Nick Cave. The culmination of this African Studies module could be a Gallery Walk of students’ African mask creations along with a presentation of the students’ recorded, original African Welcome Dances.

Unit Essential Question

What is the importance of learning and understanding African Welcome Dances, as well as the masks that African tribes create?

Real World Context

The continent of Africa is rich in dance and artistic principles. Many tribes continue to share welcome dances from the past from generation to generation and continue to create new versions in today’s society. Being able to understand these welcome dances, as well as the history of African masks, allows us to better understand who we are as individuals.

Cross-Cutting Interdisciplinary Concepts

Relationships
Diversity
Culture

Projects

Project 1: Dance Component - African Welcome Dance
In this arts integrated component, students will understand the meanings of African “Welcome” dances specific to a tribe or region in Africa. They will compare and contrast traditional “Welcome” dances to modern “Step” dances. The students will incorporate modern dance into their unique versions of a Tribal Welcome dance.

Project 2: Visual Arts Component - African Tribal Masks
In this visual arts component, students will participate in a one-of-a kind African mask adventure as they compare and contrast traditional African masks and their role within African Masquerades to the work of contemporary artist Nick Cave. Students will create a 3D African mask using a variety of materials inspired by cultural attributes from an assigned region in Africa.

Standards

Curriculum Standards

SS7G4. Students will describe the diverse cultures of the people who live in Africa.

1. Explain the differences between an ethnic group and a religious group.
2. Explain the diversity of religions within the Arab, Ashanti, Bantu, and Swahili ethnic groups.
3. Evaluate how the literacy rate affects the standard of living.

SS7H1 The student will analyze continuity and change in Africa leading to the 21st century.

2. Explain how nationalism led to independence in South Africa, Kenya, and Nigeria.
4. Explain the impact of the Pan-African movement.

National Standards

NSS-G.K-12.2

1. Understand the physical and human characteristics of places.
2. Understand that people create regions to interpret Earth’s complexity.
3. Understand how culture and experience influence people’s perceptions of places and regions.

Arts Standards

DMSPFD.4. Understands and applies music concepts to dance.

1. Recognizes how different rhythm structures are utilized by a variety of music idioms and cultures and how those rhythms influence dance styles (e.g., ballet, jazz, African).

DMSPCR.1. Demonstrates an understanding of creative and choreographic principles, processes, and structures.

1. Explores and refines partnering skills.
2. Demonstrates a variety of structures, forms, and designs (e.g., AB, ABA, canon, call-response, narrative, complimentary/contrasting shapes, symmetry).
3. Applies dance technique principles to the choreographic context.
4. Develops versatility through experimentation with various movement approaches.
5. Implements the use of props within the choreography.

DMSPCO.1. Demonstrates and understands dance in various cultures and historical periods.

1. Performs folk and/or classical dances from various cultures; describes similarities and differences in steps and movement styles.
2. Performs folk, social, and/or theatrical dancers from a broad spectrum of twentieth-century America.
3. Describe the role of dance in at least two different cultures or time periods.
4. Accesses and uses community resources (such as people, books, videos) to learn about a folk dance of a different culture or a social dance of a different time period and the cultural/historical context of that dance.

VA7MC.1 Identifies and works to solve problems through creative thinking, planning, and/or experimenting with art methods and materials.

VA7CU.1 Discovers how the creative process relates to art history.

VA7MC.3 Interprets how artists create and communicate meaning in and through their work.

VA7CU.2 Investigates and discovers personal relationship to community, culture, and world through creating and studying art.

VA7PR.3 Uses the elements and principles of design along with a variety of media, techniques and skills to produce two-dimensional and three-dimensional works of art.

National Standards

DA:Cr1.1.7.a. Compare a variety of stimuli (for example, music, observed dance, literary forms, notation, natural phenomena, personal experience/recall, current news or social events) and make selections to expand movement vocabulary and artistic expression.

VA:Cr1.2.7a. Develop criteria to guide making a work of art or design to meet an identified goal.

VA:Cr2.1.7a. Demonstrate persistence in developing skills with various materials, methods, and approaches in creating works of art or design.

Character Education

Components

Exhibiting the character trait of tolerance is one of the most important character educational components we teach to children. Tolerance is something that should be shown from children to adults alike. If we are able to appreciate others, then this naturally leads to exhibiting a tolerant attitude. In order for children to become successful adults, students need to be able to accept individual differences, negotiate and compromise. They should strive to discover and learn about people different from themselves and cultures different from their own. Most importantly, students who are able to understand that all people have value as human beings, naturally become productive members of society.
Attributes

• Exhibiting Tolerance
• Showing Respect for Other Cultures

Appendix (See Addition Resources)

• Pre/Post-Assessment
• African Studies Rubric

Credits